Курс „Интеграл. Плоские фигуры”
Производной функции[понятие: Производная функции (funktsiooni tuletis) – производная функции 𝑦 = 𝑓 (𝑥) в точке 𝑥₀ есть величина, к которой стремится отношение приращения функции к приращению аргумента, когда приращение аргумента стремится к числу 0.] y = f (x) называется величина f '(x), к которой стремится отношение приращения функции к приращению аргумента , когда приращение аргумента Δx → 0. Производная функции в точке х равна угловому коэффициенту касательной[понятие: Угловой коэффициент касательной (puutuja tõus) – угловой коэффициент прямой, являющейся касательной к графику функции.], проведенной к графику функции в точке с абсциссой х:
С помощью предела определение производной функции можно записать в виде:
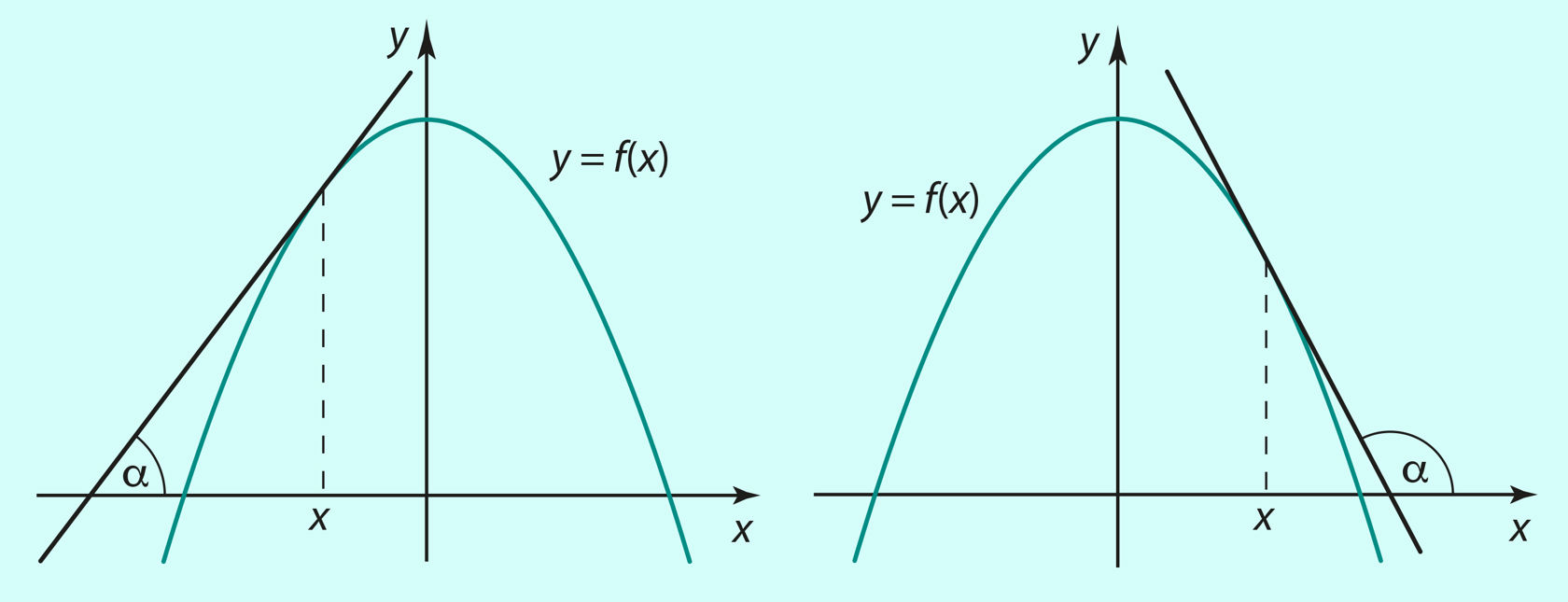 Рис. 1.1 | ||||||