Lineaarfunktsioon
Lineaarfunktsiooni esitab valem
y = ax + b,
kus ax + b on muutuja x lineaaravaldis,
milles a ja b on reaalarvud ja a ≠ 0.
Märka
Lineaarfunktsiooni graafikuks on sirge, mille algordinaat on b ja tõus a = tan α,kus α on tõusunurk.
Graafik y = b + ax
Tõusev sirge
Langev sirge
- Funktsiooni y = 7x – 9 tõus
a = ja algordinaat
b = . - Funktsiooni y = –x tõus
a = ja algordinaat
b = . - Funktsiooni y = 7 – 9x tõus
a = ja algordinaat
b = .
Pöördvõrdeline seos
Pöördvõrdelist seost esitab valem
ehk xy = k,
kus k on reaalarv ja k ≠ 0.
Märka
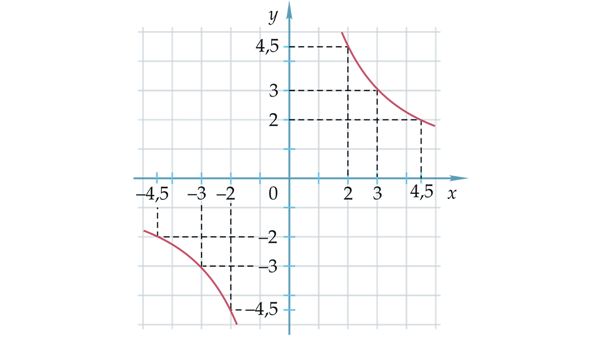
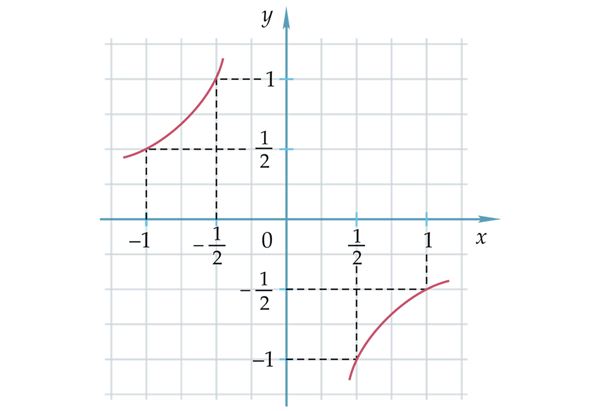
Pöördvõrdelise seose graafikuks on hüperbool.
Hüperbool
Hüperbooli harude asend sõltub konstandi k märgist.
- Kui k > 0 , siis asuvad hüperbooli harud I ja III koordinaatveerandis.
- Kui k < 0, siis asuvad hüperbooli harud II ja IV veerandis.
Mõtle
- k =
- Seose valem
y =
- k =
- Seose valem
y = –
Ruutfunktsioon
Ruutfunktsiooni esitab valem
y = ax2 + bx + c,
kus a, b ja c on reaalarvud ning a ≠ 0.
Märka
- Ruutfunktsiooni graafikuks on parabool, mis lõikab y-telge kohal c.
- Parabool on sümmeetriline telje suhtes.
Parabool
- Muuda liuguritega ruutliikme ja lineaarliikme kordaja ning vabaliikme väärtust.
- Uuri sümmeetriatelje, haripunkti ja nullkohtade asukohta.
Harjuta ja treeni
- Taksosõidu pikkus ja hind
- Läbitud tee pikkus ja aeg
- Võrdkülgse kolmnurga külg ja pindala
- Ringi raadius ja pindala
- Kindla kõrgusega prisma ruumala ja põhja pindala
- Arv ja selle absoluutväärtus
- Palvelun tarjoaa Star Cloud OÜ