Kaks vähe, kolm palju
Õppereisiks näitusele tuleb tellida sõiduk. Kui tellida kaks 7-kohalist bussi, jääb kaks kohta puudu, aga kui tellida üks 19-kohaline buss, jääb kolm kohta üle. Mitu õpilast läheb õppereisile, kui kaasas on üks õpetaja?
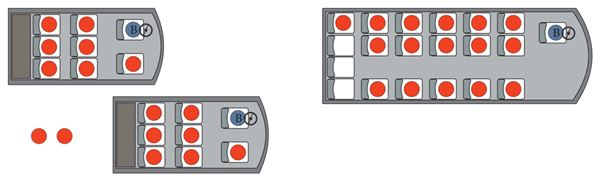
Vastus
õpilast läheb õppereisile.
Kaks muutujat
Andmed osalejate arvu kohta
Ühel päeval osales näitusel 220 inimest. Nende seas oli õpilasi ja täiskasvanuid.
Seda lauset saab sümbolites üles kirjutada
x + y = 220,
kus x tähistab õpilaste arvu, y tähistab täiskasvanute arvu.
Kirja on pandud kahe muutujaga lineaarvõrrand.
Aga täiskasvanute ja õpilaste arve võis olla mitmesuguseid. Näiteks 100 täiskasvanut ja 120 õpilast, sest
100 + 120 = 220
või 219 täiskasvanut ja 1 õpilane, sest
219 + 1 = 220
või veel mitu erinevat varianti.
Andmed kogunenud rahasumma kohta
Näitusepilet maksis õpilastele 1,50 € ja 4,00 € täiskasvanutele. Sellel päeval, kui näitusel käis 220 inimest, saadi piletimüügist 550 €.
Seda lauset saab sümbolites üles kirjutada
1,5 · x + 4 · y = 550,
kus 1,5 · x on õpilaste piletitest saadud raha ja 4 · y on täiskasvanute piletitest saadud raha.
Kirja on pandud kahe muutujaga lineaarvõrrand.
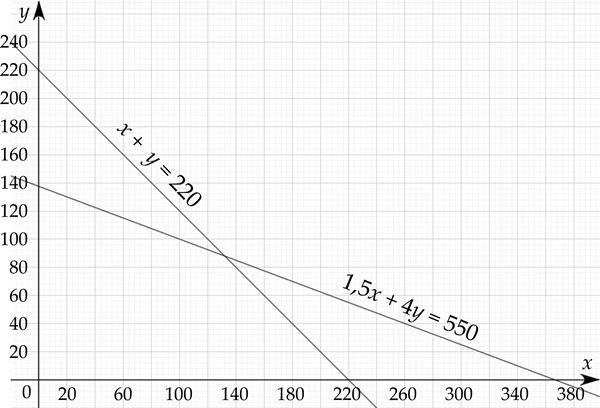
Märka
Näitusel käis sellel päeval 132 õpilast ja 88 täiskasvanut.
Kui näitusel oleks käinud 100 õpilast ja 120 täiskasvanut, siis oleks kogunenud 630 €.
Kui näitusel oleks käinud 200 õpilast ja 20 täiskasvanut, siis oleks kogunenud 380 €.
Kahe muutujaga lineaarvõrrandi üldkuju on ax + by = c,
kus a, b ja c on arvud.
Kahe muutujaga lineaarvõrrandi lahend
Erinevat tüüpi võrrandid aitavad kirjeldada erinevaid olukordi, kuid nõuavad erinevaid lahendusmeetodeid.
Ühe muutujaga võrrand on lineaarvõrrand, näiteks 3x + 7 = 12. Ühe muutujaga lineaarvõrrandil on täpselt üks lahend, kahe muutujaga võrrandi lahendiks on lõpmatu arv arvupaare.
Näide 1
Kahe muutujaga võrrandi 2x + y = 8 lahendiks sobivad arvupaarid
- (1; 6), sest 2 · 1 + 6 = 8
- (3; 2), sest 2 · 3 + 2 = 8
- (12; –16), sest 2 · 12 – 16 = 8
- (–1; 10), sest 2 · (–1) + 10 = 8
- (–9,5; 27), sest 2 · (–9,5) + 27 = 8
- jne,
Lahendiks sobivaid arvupaare on lõpmatult, sest alati saab ühe muutuja asemele valida ükskõik missuuguse arvu. Seose kaudu saab arvutada teise muutuja väärtuse.
Kahe muutujaga võrrandi ax + by = c kõik arvupaarid, mis kahe muutujaga lineaarvõrrandisse sobivad, moodustavad sirge tasandil.
Kahe muutujaga võrrandi ax + by = c saab avaldada lineaarfunktsiooni kujul
Näide 2
- y = 3 – x on sama, mis kahe muutujaga võrrand .
Üks sobiv lahend on arvupaar . - y = x + 3 on sama, mis kahe muutujaga võrrand .
Üks sobiv lahend on arvupaar . - y = – x – 3 on sama, mis kahe muutujaga võrrand .
Üks sobiv lahend on arvupaar .
Harjutan ja lahendan
- 3xy = 1
- (3x – 5)² = 2
- x² – y² = 0
- 4 – x = 0
- 3x – 5y = 2
- 0,5x + 3 = 1
- x – y = 0
- 3x – 5 = 2
- 0,5x + 3 = y
Märka
Kahe muutujaga on juba tutvutud lineaarfunktsioonide juures. Seepärast on hea meelde tuletada
- lineaarfunktsiooni mõistet,
- sirge joonestamist kahe punkti meetodil,
- sirge joonestamist tõusu ja algordinaadiga,
- sirge joonestamist, kasutades nihet.
- (–10; 29)
- (2; 7)
- (0; 2)
- (0,1; 30,7)
- (3; 1)
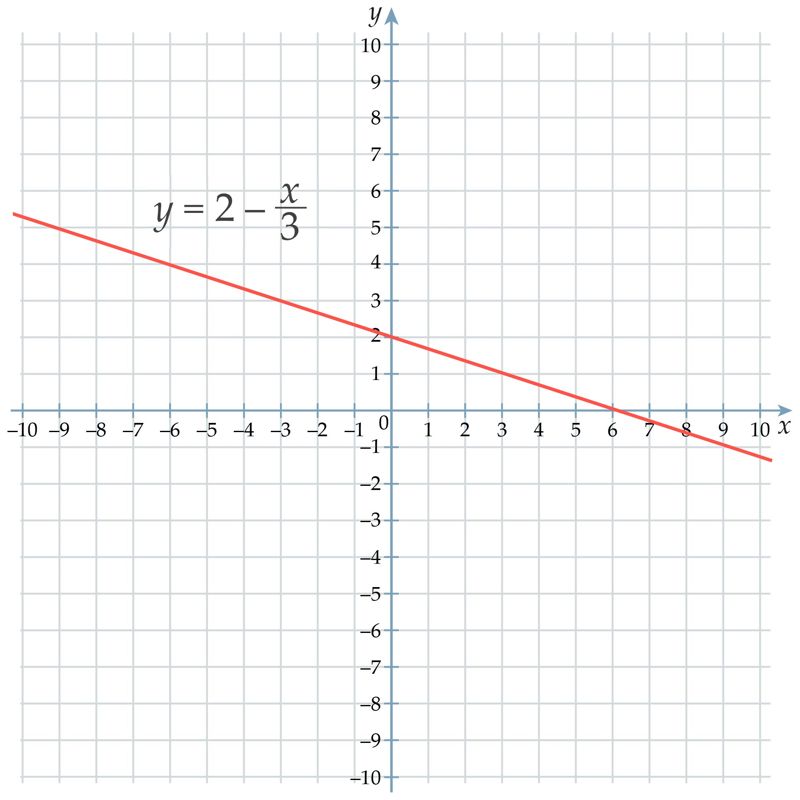
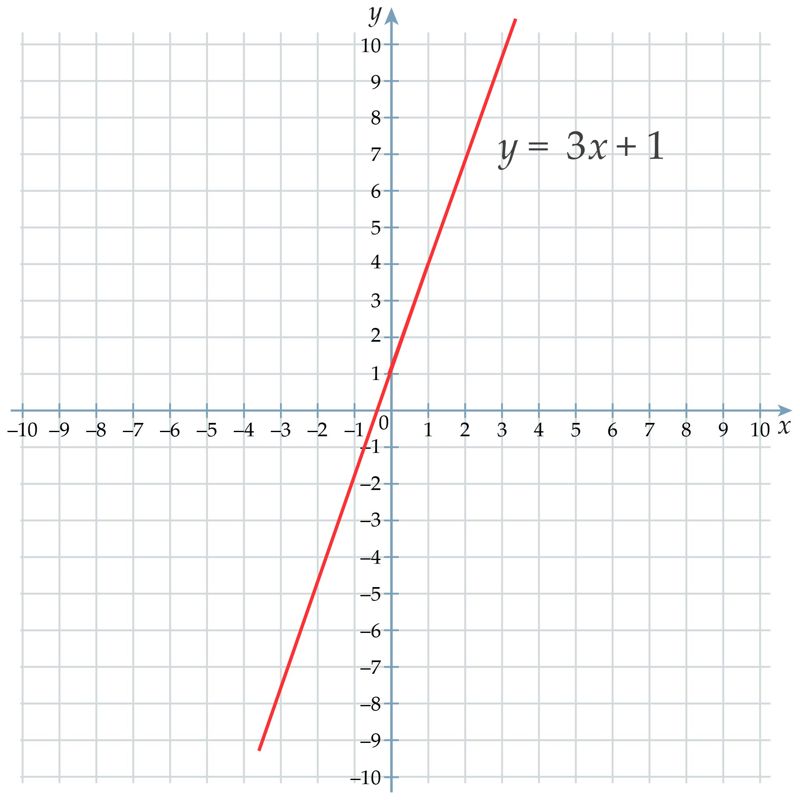
- (–9,9; 5,3 )
- (6; 0)
- (–5,7; –9,5)
- (15; –3)
- (7; –4)
- (0; 0)
- (0; 1)
Reeglid ja valemid
- Võrrand, milles esineb 2 erinevat tundmatut esimeses astmes, nimetatakse kahe tundmatuga lineaarvõrrandiks.
- Iga kahe tundmatuga lineaarvõrrandi saab teisendada kujule ax + by = c.
Antud lineaarvõrrand on
2x + 4y = 8
x – y = 17,5
y = 0,4x – 1
ax + by = c kus, a, b, c on arvud
