Peatükk 3.1 (Matemaatika 7. kl)

Hulgad

Peatükk õpetab

  • a ∈ A – element a kuulub hulka A
  • a ∉ A – element a ei kuulu hulka A
  • ∅ – tühja hulka tähistav märk 
Seotud sisu
Muud tegevused

Mõned tuttavad hulgad

Siin on esemete hulk tähistatud tähega B, selles hulgas on 5 elementi
Siin on erinevad hulgad, mis kirjeldavad Euroopa riike
Lõplik hulk A koosneb kolmest suurusest, mis on tähistatud tähtedega a, b ja c 

Arutle

  • Milline on pliiatsite hulk sinu pinalis?
  • Milline on õpetajate hulk sinu klassis?
  • Milline on poiste hulk sinu klassis?
  • Milline on logiseva jalaga toolide hulk sinu klassis?
  • Mitu elementi on hulgas, milles on sinu kooli nime tähed?
Seotud sisu
Muud tegevused

Hulgad

  • Eelnevates näidetes oli tegemist lõplike hulkadega, sest need koosnesid lõplikust arvust elementidest.

Näiteks

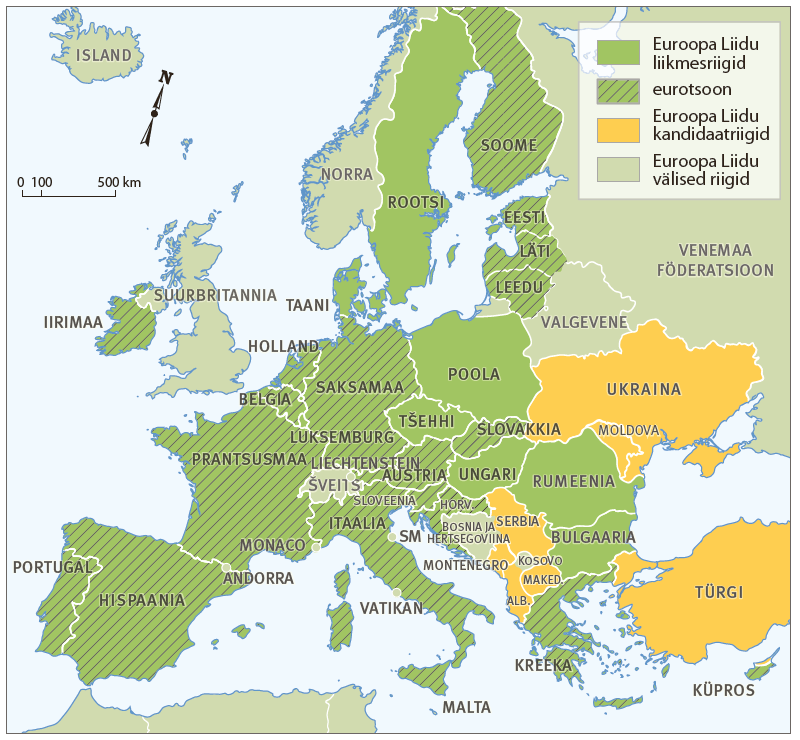
Loomaaia loomade hulk, Tallinna taksode hulk jms on lõplikud hulgad.

  • Kui aga hulk sisaldab lõpmatult palju elemente, siis on see lõpmatu hulk.

Näiteks

Sirge punktide hulk on lõpmatu. Naturaalarvude hulk 0, 1, 2, 3, ... on lõpmatu.

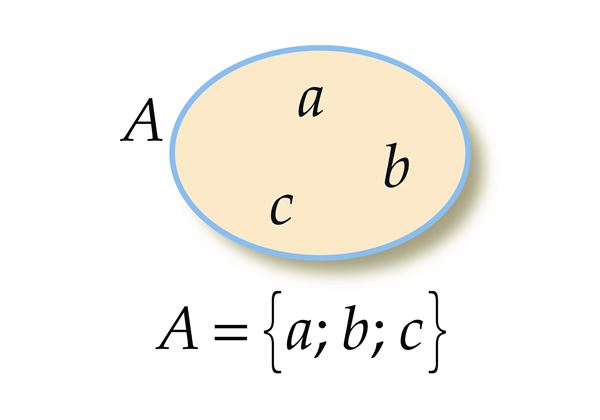
Hulga all mõistetakse objektide kogumit.

Neid objekte nimetatakse hulga elementideks.

Märka

  • Hulka tähistatakse suure tähega – A, B, C jne.
  • Lõplikku hulka saab iseloomustada tema elementide loetelu kaudu
    A = {2; 3; 5; 7; 11}.​

Näide. Algarvude sõelumine

Arvu 2 ja 100 000 000 vahel on 1 270 607 algarvu. Algarvude hulk on lõpmatu
Kõigi liivaterade hulk maakeral on lõplik hulk. Selle elementide arv on väga suur, kuid hulk on sellegi poolest lõplik

Elemendi kuuluvust hulka tähistatakse märgiga ∈.

Elemendi mittekuuluvust hulka tähistatakse märgiga ∉. 

4 ∉ A tähendab, et element 4 ei kuulu hulka A.

Hulka, kus ei ole ühtegi elementi, nimetatakse tühjaks hulgaks ja tähistuseks on märk ∅.

Arutle

  1. Majade hulk suurlinnas on  hulk.
  2. K = {3; 6; 9; 12; ...} (st kolmega jaguvad arvud) on  hulk.
  3. M = {0,05; 0,5; 5; 55; 555} on  hulk.
  4. Paarisarvude hulk on  hulk.
  5. Algarvude hulk on  hulk.
  6. Taevatähtede arv on  hulk.
  7. Kümnendmurdude hulk on  hulk.
  8. Tähtede arv raamatus on  hulk.

On antud hulk A = {0; 2; 4; 6; 8}. 

      • 1 ∈ A
      • A = ∅
      • 6 ∉ A
      • 5 ∉ A
      • A ≠ ∅
      • 0 ∈ A

      On antud hulgad A = {1; 3; 5} ja B = {2; 4, 6}. 

      Hulga C elementideks on kõikvõimalikud hulkade A ja B elementide summad kasvavas järjekorras. 

      • Vähim võimalik summa on .
      • Suurim võimalik summa on .
      • Hulga C elemendid kasvavas järjekorras
        C = {; ; ; ; }.  

      On antud hulgad K = {2; 3; 5} ja L = {2; 3}.  

      Hulga M elementideks on kõikvõimalikud hulkade K ja L elementide korrutised. 

       M = {; ; ; ; } 

      Hulgad, osahulgad ja element
      Seotud sisu
      Muud tegevused

      Harjutan ja lahendan

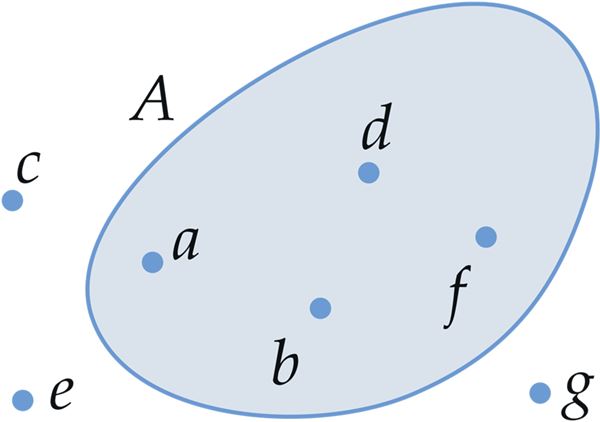
      a   A

      b   A

      c   A

      d   A

      e   A

      f   A

      g  A

      Arvuta avaldise 3 ⋅ a + a : 4 − 1 väärtused, kui 
      a ∈ {8; 12; 10; 26}. 

      1. Kui a = 8, siis
        3 ⋅ a + a : 4 − 1 = .
      2. Kui a = 12, siis
        3 ⋅ a + a : 4 − 1 = .
      3. Kui a = 10, siis
        3 ⋅ a + a : 4 − 1 = .
      4. Kui a = 26, siis
        3 ⋅ a + a : 4 − 1 = .

      Antud on avaldise 2 ⋅ a + b väärtused, kui
      a ∈ {3; 5; 7} ja b ∈ {2; 4}.

      1. Kui 2 ⋅ a + b = 12, siis
        a =  ja b = . 
      2. Kui 2 ⋅ a + b = 8, siis
        a =  ja b = . 
      3. Kui 2 ⋅ a + b = 10, siis
        a =  ja b = .
      4. Kui 2 ⋅ a + b = 18, siis
        a =  ja b = .
      5. Kui 2 ⋅ a + b = 14, siis
        a =  ja b = .
      6. Kui 2 ⋅ a + b = 16, siis
        a =  ja b = . 
      Seotud sisu
      Muud tegevused

      Reeglid ja valemid

      • a ∈ A – element a kuulub hulka A 
      • a ∉ A – element a ei kuulu hulka A 
      • ∅ – tühja hulka tähistav märk
      • Loe m ∈ N  
      • Loe m ∉ N  
      • Loe N = ∅ 
      Seotud sisu
      Muud tegevused
      Palun oota