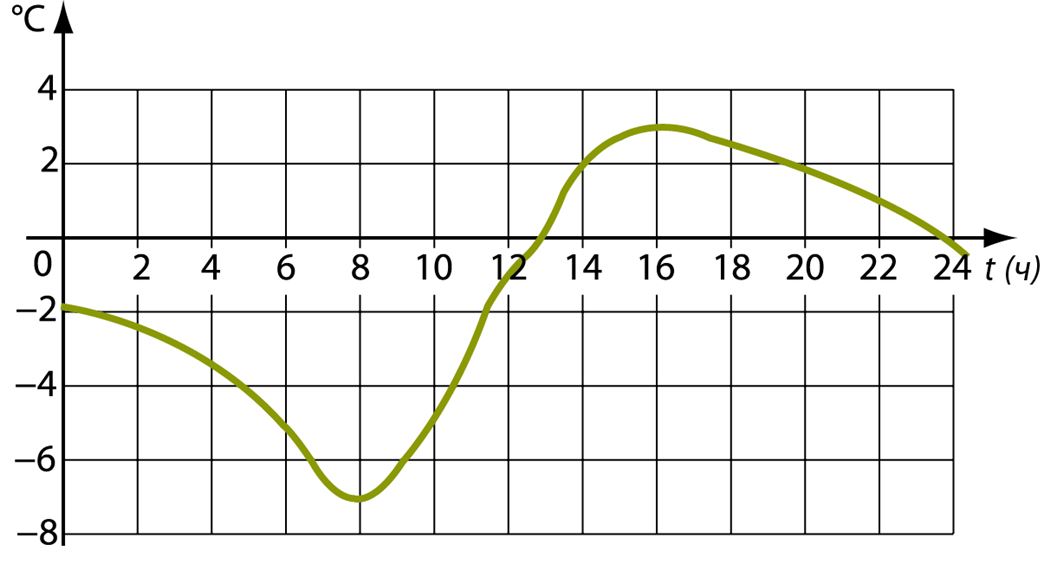
Мы встречаемся с числами повсюду. Каждый день нам приходится что-нибудь подсчитывать, измерять и вычислять. Вспомни, что ты сегодня подсчитал, измерил или вычислил.

Числа 0; 1; 2; 3; ... называются натуральными числами[понятие: Натуральные числа – (Naturaalarvud) числа 0; 1; 2; 3; ...]. Ими ты наверняка пользовался до того, как начал ходить в школу, но познакомился с их свойствами только в начальных классах. Натуральные числа всегда можно складывать и перемножать, но при вычитании или делении не всегда получается натуральноое число.
Для того, чтобы можно было вычесть из меньшего числа большее, вводят отрицательные числа, то есть числа, противоположные натуральным. Выполнять действия с этими числами ты научился в предыдущем учебном году. Натуральные числа и им противоположные числа вместе образуют множество целых чисел[понятие: Целые числа – (Täisarvud) общее наименование натуральных чисел и противоположных им чисел.].
Для того, чтобы всегда стало возможным деление двух целых чисел (кроме деления на нуль), нужно ввести положительные и отрицательные дробные числа. Дробные и целые числа вместе образуют множество рациональных чисел[понятие: Рациональные числа – (Ratsionaalarvud) общее наименование всех целых и дробных чисел.]. В этой главе мы научимся выполнять действия с рациональными числами.

Усвоив материал этой главы, ты будешь знать, что означают выражения:
- рациональное число,
- противоположное число,
- модуль числа,
- степень числа,
а также будешь уметь:
- упорядочивать рациональные числа;
- складывать, вычитать, умножать и делить эти числа;
- пользоваться правилами порядка выполнения действий, а также законами сложения и умножения;
- вычислять расстояние между двумя точками числовой оси;
- вычислять значения буквенных выражений, содержащих рациональные числа;
- возводить числа в степень;
- пользоваться степенями числа 10 для записи очень больших чисел;
- решать текстовые задачи и простейшие уравнения.