Параграф 2.1 (Mathematics, Grade 9)

Replacing an Operation with Other Operations

This chapter covers:

  • techniques for mental multiplication and division
  • approximations of the number π
Еще на эту тему
Другие действия

0.5 and 2

Multiplying by 0.5 and dividing by 2 give the same result.

Dividing by 0.5 and multiplying by 2 give the same result.

Notice

n is used as a placeholder for a generalised example. When solving specific equations, it is substituted with the necessary number.

  •   n:2 = n2=12·n
  • n:0.5=n:12=n·21=
      =2n1=2n

Example 1

  • 52 : 0.5 = 52 · 2 = 104
  • 43 · 0.5 = 43 : 2 = 21.5

Drag the operations to their corresponding columns.

      • 18 · 0.5
      • 17 · 2
      • 0.5 : 0.5
      • 32 : 0.5
      • 0.5 · 0.5
      • 0.5 · 23
      • 12 : 2
      • 65 : 0.5

      The answers to the operations are given below. Select the numbers among them that are not the answers to the given operations.

      • 8.5
      • 11.5
      • 64
      • 6
      • 1
      • 32.5
      • 130
      • 0.25
      • 46
      • 9
      • 25
      • 34
      • 2 : 0.5
      • 1 : 0.5
      • 0.2 · 0.5
      • 0.2 : 0.5
      • 0.5 · 0.5
      • 2 · 0.5
      • 150 · 0.5
      • 15 : 0.5
      • 150 : 0.5
      • 1.5 : 0.5
      • 15 · 0.5
      Еще на эту тему
      Другие действия

      Multiplying by 1.5 and 2.5

      Multiplying by 3 and then dividing by 2 gives the same result as multiplying by 1.5.

      Multiplying by 5 and then dividing by 2 gives the same result as multiplying by 2.5.

      Notice

      n is a placeholder for a freely chosen number.

      • 1.5·n=112·n =
        = 32·n = 3n2 =n2·3= ​
        = n:2⋅3 ​
      • 2.5·n=212·n=
        ​ =52·n=5n2=n2·5 =
        ​  =n:2·5

      Example 2

      • If I need to multiply 14 by 1.5, I first divide 14 by 2 to equal 7, and then multiply 7 by 3 to equal 21, so I get 1.5 · 14 = 21.
      • ​​If I need to multiply 72 by 2.5, I first divide 72 by 2 to equal 36, and then multiply 36 by 5 to equal 180, so I get 2.5 · 72 = 180.
      1. 1.5 · 28 =  = 
      2. 1.5 · 46 =  = 
      3. 1.5 · 14 =  = 
      4. 1.5 · 17 =  = 
      5. 1.5 · 61 =  = 
      6. 2.5 · 8 =  = 
      7. 2.5 · 22 =  = 
      8. 2.5 · 34 =  = 
      9. 2.5 · 52 =  = 
      10. 2.5 · 9 =  = 
      1. 2.5 · 12 = 12 : 2 ·  = 
      2. 1.5 · 12 = 12 : 2 ·  = 
      3. 3.5 · 12 = 12 : 2 ·  = 
      4. 4.5 · 12 = 12 : 2 ·  = 
      5. 5.5 · 12 = 12 : 2 ·  = 
      6. 3.5 · 26 = 26 : 2 ·  = 
      7. 4.5 · 13 = 13 : 2 ·  = 
      8. 5.5 · 84 = 84 : 2 ·  = 

      Notice

      ⍰.5 ·n=2 ·⍰ +1 2·n= = n2· ( 2· ⍰+ 1 ) = =n :2· ( 2· ⍰+ 1 )

      Еще на эту тему
      Другие действия

      Divisiding by 25

      Multiplying by 4 and then dividing by 100 gives the same result as dividing by 25.

      Notice

      n is a freely chosen number.

      n:25=n:1004=n·4100

      300 : 25 = 

      850 : 25 = 

      625 : 25 = 

      175 : 25 = 

      105 : 25 = 

      70 : 25 = 

      90 : 25 = 

      275 : 25 = 

      Еще на эту тему
      Другие действия

      Multiplying by 11

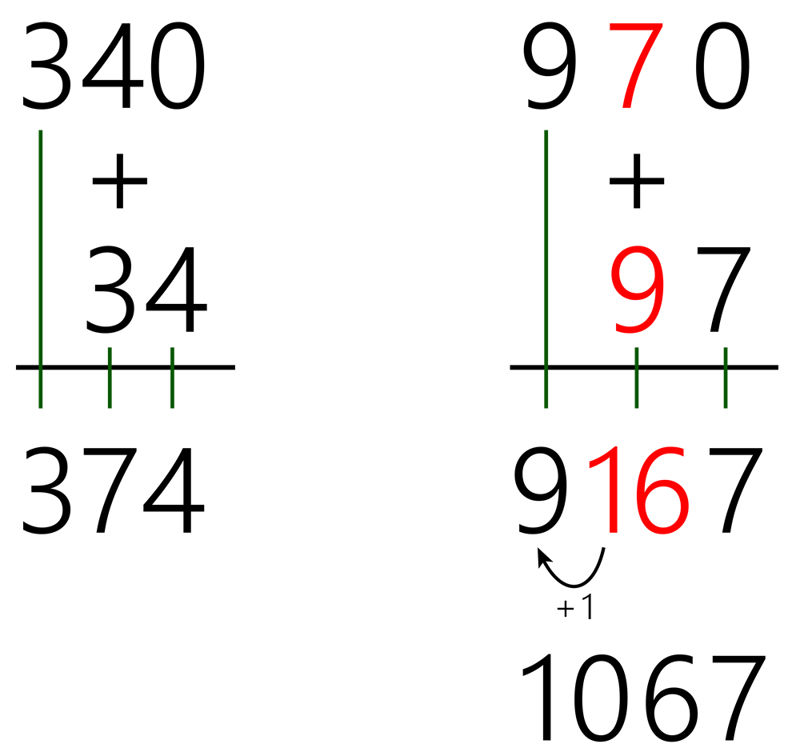
      When multiplying a two-digit number by 11, we know that 11 = 10 + 1, so 11 · n = (10 + 1) · n = 10 · n + n.

      Example 3

      11 · 34  and 11 · 97

      Replacing the multiplication of 11 · 34 and 11 · 97 with addition when doing a mental calculation.

      11 · 33 = 

      11 · 35 = 

      11 · 62 = 

      11 · 75 = 

      11 · 98 = 

      11 · 78 = 

      22 · 31 = 

      22 · 45 = 

      22 · 23 = 

      22 · 14 = 

      22 · 71 = 

      22 · 88 = 

      Еще на эту тему
      Другие действия

      Practice and solve

      We know that the number π is the quotient of the length of a circle and its diameter. The closest fraction to this value is
      π ≈  22 7 ≈ 3.1428571... .

      1. If d = 3, then
        C ≈  7  ≈ .
      2. If d = 12, then
        C ≈  7  ≈ .
      3. If d = 50, then
        C ≈  7  ≈ .
      4. If d = 28, then
        C ≈  7  ≈ .
      5. If d = 41, then
        C ≈  7 ≈ .
      6. If d = 39, then
        C ≈  7  ≈ .
      Find the circumference of 50 cents.

      How can you make sure? You can, for example, roll the coin over a ruler.

      π ≈  22 7

      Trees are companions to humanity. Their wood, roots and leaves are used around the world. As long as we plant seeds and care for them, and not take trees that are essential to their ecosystem (such as those offering shelter to animals), we can continue to have a respectful relationship with trees. One example of this is waiting for a tree to be large enough to yield much wood, and old enough to have contributed much to their ecosystem.

      • A mature pine has a diameter of 28 cm and a circumference of  cm.
      • A mature black poplar has a diameter of 182 cm and a circumference of  cm.
      • A pine tree is ready to harvest when their diameter is the longer side of a sheet of  paper. Their girth is then around  cm (rounded up to a whole number).
      • The oak tree is ready to harvest when they are 
      • Birch is ready to harvest when they are 
      • The fir tree ready to harvest when they are 
      • The alder is ready to harvest when they are 
      • The pine tree is ready to harvest when they are 
      • The hanging alder is ready to harvest when they are 
      Еще на эту тему
      Другие действия

      Rules and formulas

      • n·0.5=n2=n:2
      • n:0.5=2n
      • 1.5n=3n2=n:2·3
      • n:25=n:1004=n·4100=   n:100·4
      • 11n=(10+1)n=10n+n
      Еще на эту тему
      Другие действия
      Пожалуйста, подождите