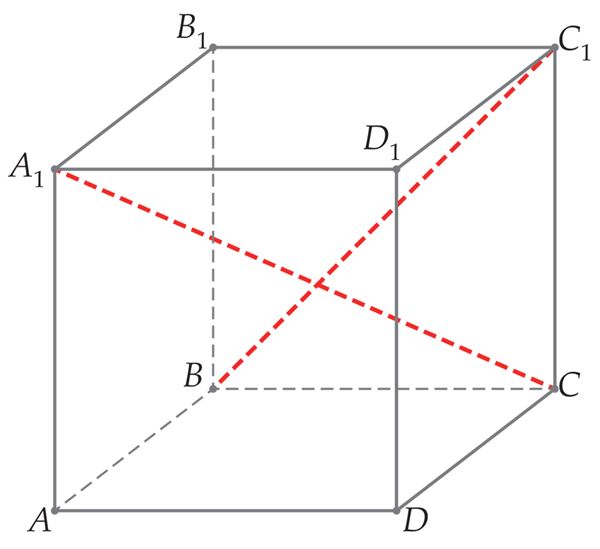
Punkti kaugus
Ruumigeomeetria ehk stereomeetria tegeleb ruumiliste kehade ja nende lõigetega. Alustame sammsammulist üleminekut tasapinnalt kolmemõõtmelisse ruumi.
Tasandigeomeetria
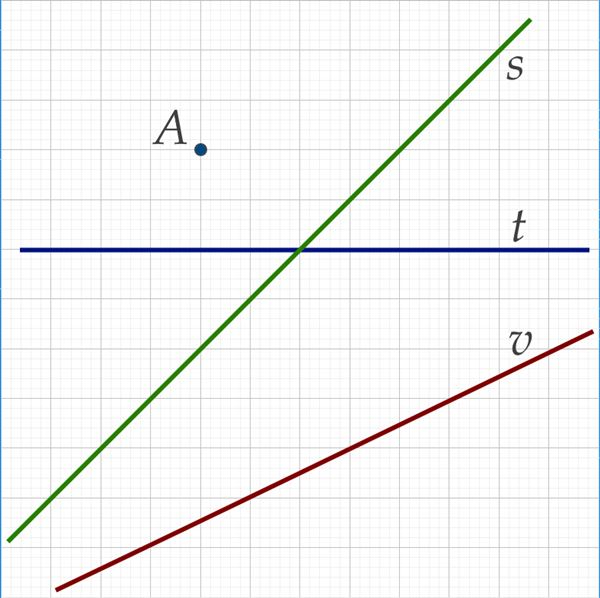
- Kui kaugel on punkt sirgest[mõiste: punkti kaugus sirgest – sellest punktist sirgeni tõmmatud ristlõigu pikkus. Selle ristõigu teine otspunkt on punkti projektsioon sellel sirgel].
Ruumigeomeetria
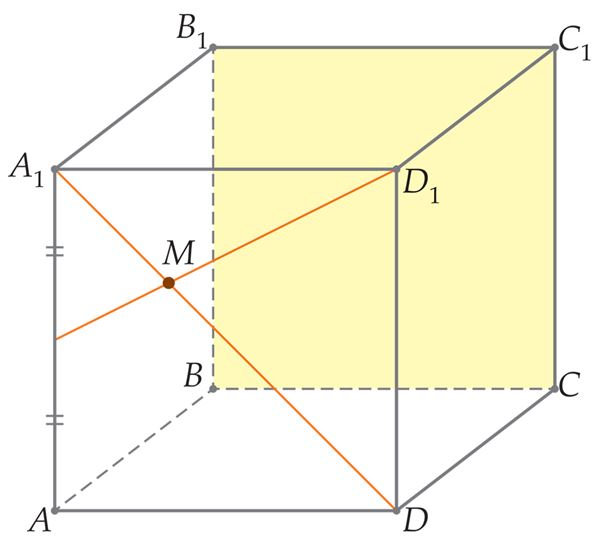
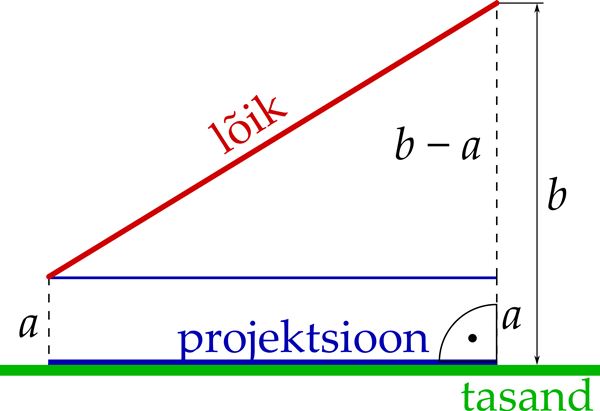
- Kui kaugel on punkt tasandist[mõiste: punkti kaugus tasandist – sellest punktist tasandini tõmmatud ristlõigu pikkus].
Näide
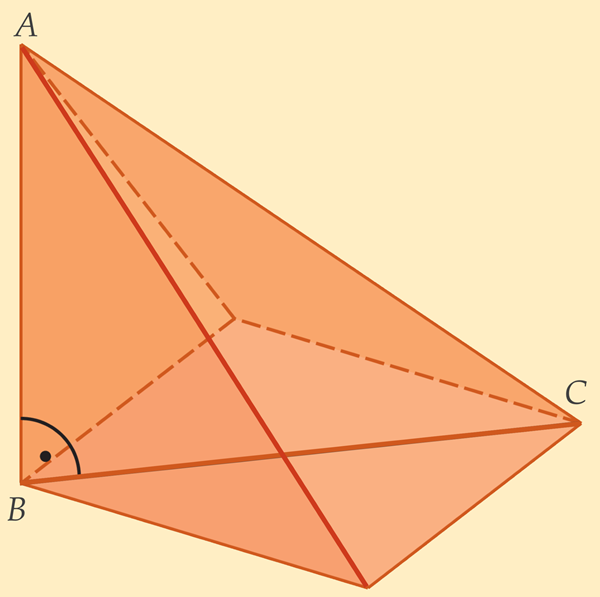
Projektsiooni pikkus
Tasandigeomeetria
- Kui pikk on lõigu projektsioon sirgel?[mõiste: lõigu projektsioon sirgel – lõigu algus- ja lõpp-punkti projektsioonide vahelise lõigu pikkus sellel sirgel]
Ruumigeomeetria
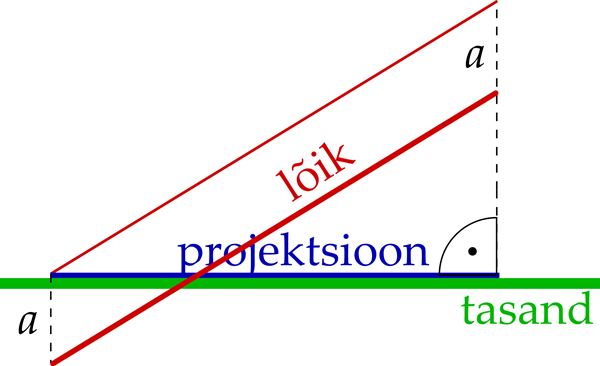
- Kui pikk on lõigu projektsioon tasandil?[mõiste: lõigu projektsioon tasandil – lõigu algus- ja lõpp-punkti projektsioonide vahelise lõigu pikkus sellel tasandil]
Näide
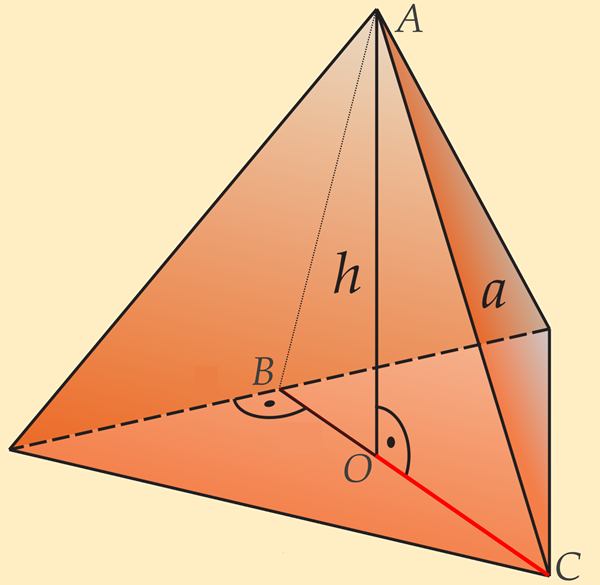
Nurga suurus
Tasandigeomeetria
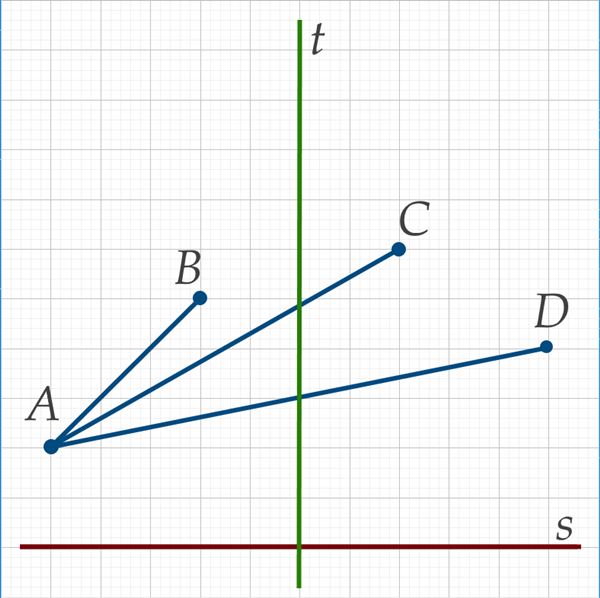
- Kui suur on nurk kahe lõigu vahel?
Ruumigeomeetria
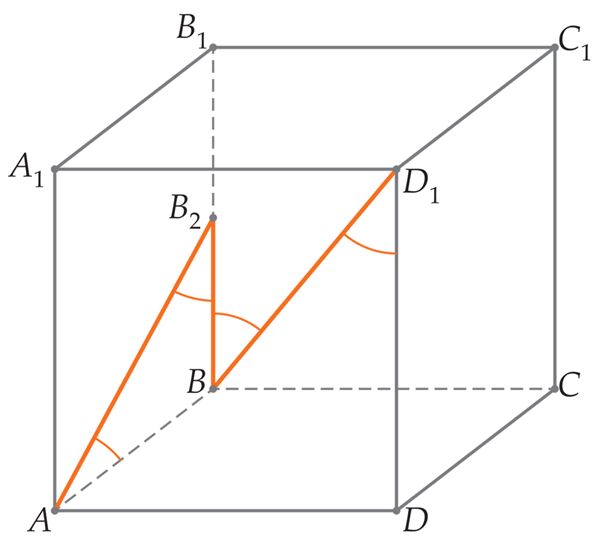
Kui suur on nurk
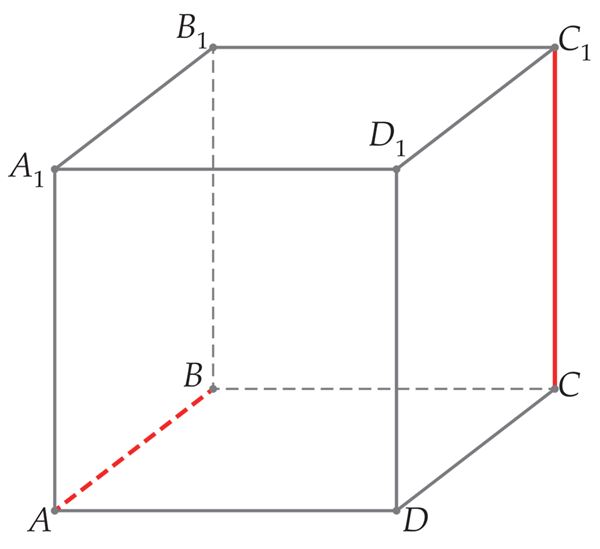
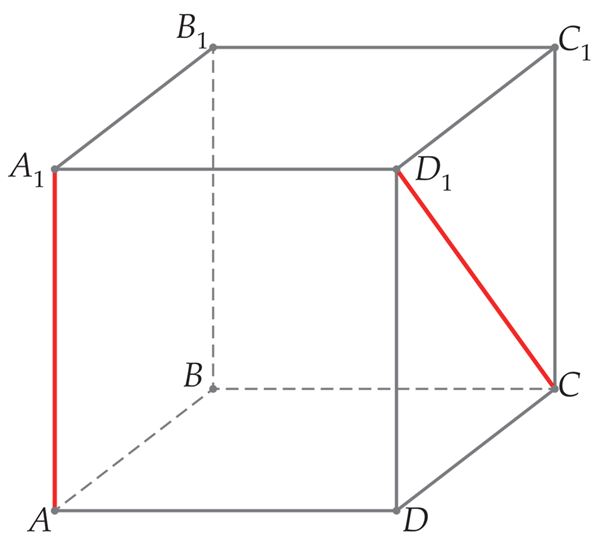
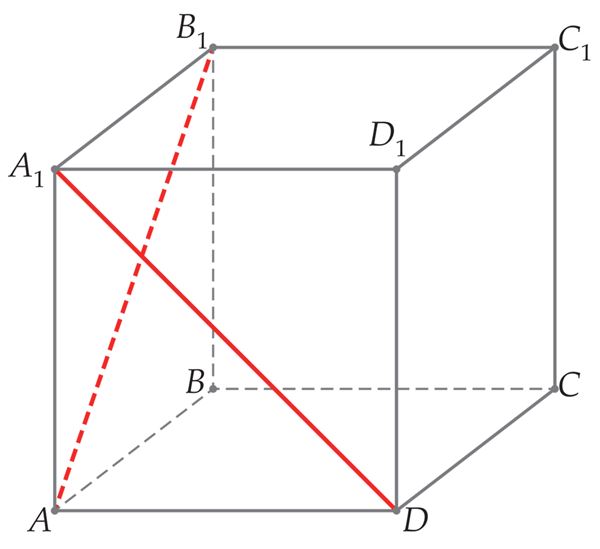
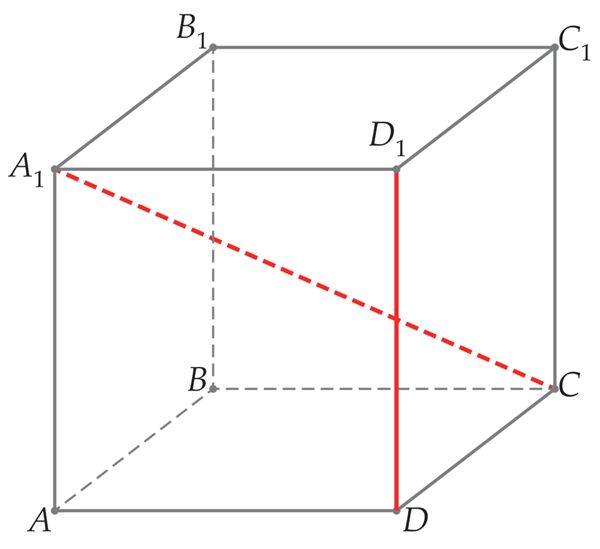
- kiivsirgete vahel,[mõiste: nurk kiivsirgete vahel – nurk ühe antud sirge jasellise temaga lõikuva sirge vahel, mis on paralleelne teisega antud sirgetest]
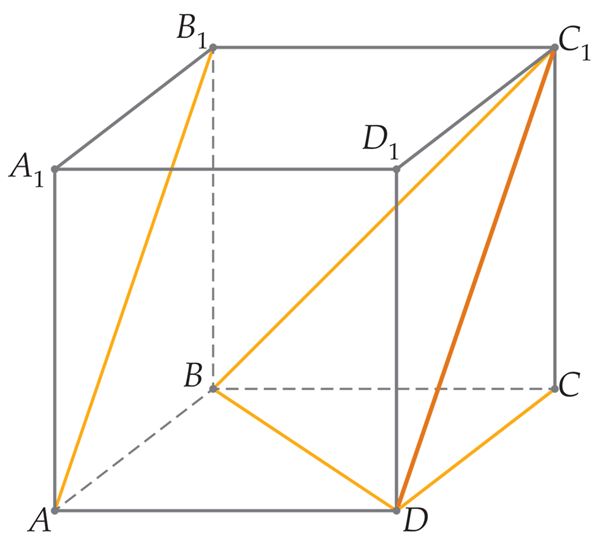
- lõigu ja tasandi vahel[mõiste: nurk sirge ja tasandi vahel – nurk sirge ja tema projektsiooni vahel sellel tasandil],
- kahe lõikuva tasandi vahel?[mõiste: nurk kahe tasandi vahel – lõikuvate tasandite lõikesirgega ristuvale sirgete vaheline nurk, kui üks neist asub ühel, teine teisel tasandil]
Näide
Harjuta ja treeni
Märka
- Väljaspool tasandit asuvast punktist A on tasandini tõmmatud kaldlõik pikkusega 8. Leia punkti A kaugus tasandist, kui nurk lõigu ja tasandi vahel on 30°.
Vastus. Punkti kaugus tasandist on . - Väljaspool tasandit asuvast punktist B on tasandini tõmmatud kaldlõik pikkusega 6. Leia punkti B kauguse ruut tasandist, kui nurk lõigu ja tasandi vahel on 60°.
Vastus. Kauguse ruut tasandist on .
- Kui muuta lõigu pikkust ja jätta samaks lõigu otspunktide kaugused tasandist, siis lõigu keskpunkti kaugus tasandist
- Kui pikendada lõiku üle otspunktide võrdselt ja jätta kaldenurk samaks, siis lõigu keskpunkti kaugus tasandist
- Lõigu üks otspunkt on fikseeritud. Kui siis muuta lõigu kaldenurka ja jätta lõigu pikkus samaks, siis lõigu keskpunkti kaugus tasandist
Märka
Nurk kiivsirgete vahel – nurk ühe antud sirge ja sellise temaga lõikuva sirge vahel, mis on paralleelne teisega antud sirgetest.